5. Jangkauan Data, Jangkauan Antarkuartil, dan Simpangan Kuartil a. Jangkauan Data
Jangkauan data atau disebut juga rentang data adalah selisih antara datum terbesar dan datum terkecil. Jika jangkauan data dinotasikan J, datum terbesar xn, dan datum terkecil x1 maka
J=xn - x1
Jangkauan antarkuartil atau disebut juga rentang interkuartil adalah selisih kuartil atas (Q3) dan kuartil bawah (Q1). Jika jangkauan antarkuartil dinotasikan JK maka
JK=Q3 - Q1
Perbedaan antara jangkauan data dan jangkauan antarkuarti ljangkauan antarkuartil merupakan ukuran penyebaran data yang lebih baik daripada rentang sebab JK mengukur rentang dari 50% data yang di tengah.
Selain jangkauan dan jangkauan antarkuartil, dikenal pula simpangan kuartil atau rentang semi-interkuartil. Simpangan kuartil (SK) adalah setengah dari K jangkauan antarkuartil (JK).
 b. Pencilan (Outlier)
b. Pencilan (Outlier) Nilai statistik jangkauan (J) dan J jangkauan antarkuartil (JK) dapat digunakan untuk memperoleh gambaran tentang K penyebaran data dengan cepat. Untuk keperluan tersebut didefinisikan satu langkah sebagai berikut.
Definisi :
Satu langkah (L) adalah satu setengah kali panjang jangkauan antarkuartil (JK). Secara matematis, ditulis
 Nilai yang letaknya satu langkah di bawah Q1 dinamakan pagar dalam (PD). Adapun nilai yang letaknya satu langkah di atas Q3 dinamakan pagar luar (PL)
Nilai yang letaknya satu langkah di bawah Q1 dinamakan pagar dalam (PD). Adapun nilai yang letaknya satu langkah di atas Q3 dinamakan pagar luar (PL) Semua data yang nilainya kurang dari pagar dalam atau lebih dari pagar luar disebut pencilan. Pencilan adalah datum yang memiliki karakteristik berbeda dari datum lainnya. Dapat dikatakan bahwa pencilan merupakan datum yang tidak konsisten dalam kumpulan data.
Semua data yang nilainya kurang dari pagar dalam atau lebih dari pagar luar disebut pencilan. Pencilan adalah datum yang memiliki karakteristik berbeda dari datum lainnya. Dapat dikatakan bahwa pencilan merupakan datum yang tidak konsisten dalam kumpulan data.

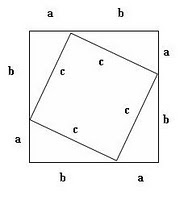 Luas persegi besar = Luas persegi kecil + 4 Luas segitiga
Luas persegi besar = Luas persegi kecil + 4 Luas segitiga


